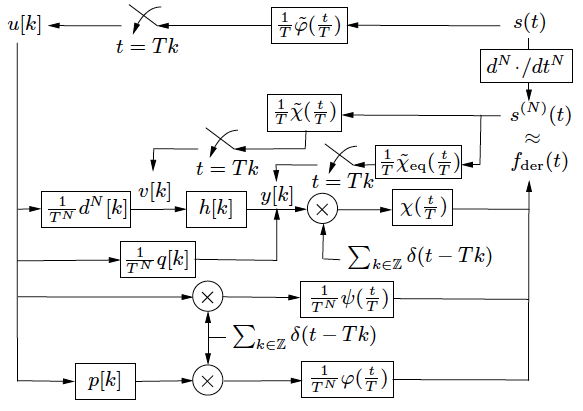
We present a general Fourier-based method which provides an accurate prediction of the approximation error, when the derivative of a signal s(t) is continuously reconstructed from uniform point samples or generalized measurements on s. This formalism applies to a wide class of convolution-based techniques. It provides a key tool, the frequency error kernel, for designing computationally efficient reconstruction schemes which are near optimal in the least-squares sense.

Top