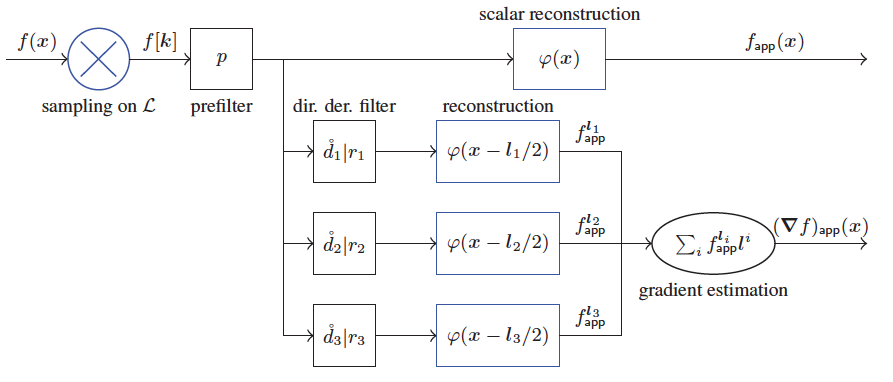
We investigate the use of a Fourier-domain derivative error kernel to quantify the error incurred while estimating the gradient of a function from scalar point samples on a regular lattice. We use the error kernel to show that gradient reconstruction quality is significantly enhanced merely by shifting the reconstruction kernel to the centers of the principal lattice directions. Additionally, we exploit the algebraic similarities between the scalar and derivative error kernels to design asymptotically optimal gradient estimation filters that can be factored into an infinite impulse response interpolation prefilter and a finite impulse response directional derivative filter. This leads to a significant performance gain both in terms of accuracy and computational efficiency. The interpolation prefilter provides an accurate scalar approximation and can be re-used to cheaply compute directional derivatives on-the-fly without the need to store gradients. We demonstrate the impact of our filters in the context of volume rendering of scalar data sampled on the Cartesian and Body-Centered Cubic lattices. Our results rival those obtained from other competitive gradient estimation methods while incurring no additional computational or storage overhead.

Top

(49 out of 185 accepted)

Top