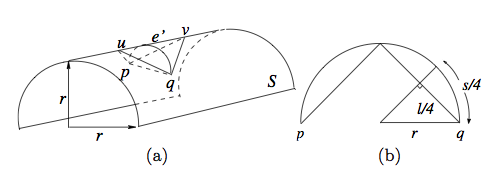
We define a Delaunay mesh to be a manifold triangle mesh whose edges form an intrinsic Delaunay triangulation or iDT of its vertices, where the triangulated domain is the piecewise flat mesh surface. We show that meshes constructed from a smooth surface by taking an iDT or a restricted Delaunay triangulation, do not in general yield a Delaunay mesh. We establish a precise dual relationship between the iDT and the Voronoi tessellation of the vertices of a piecewise flat (pwf) surface and exploit this duality to demonstrate criteria which ensure the existence of a proper Delaunay triangulation.

Top